問1　2018年9月基礎

Ａさん（45歳）は、65歳から15年間にわたって毎年600千円を受け取るために、65歳までの20年間、年金原資を毎年均等に積み立てることを考えている。この場合、45歳から65歳までの20年間の毎年の積立額はいくらになるか。下記の係数表を利用して算出した次の金額のうち、最も適切なものを選びなさい。
なお、積立期間および取崩期間中の運用利回り（複利）は年２％とし、積立ておよび取崩しは年１回行うものとする。また、計算結果は千円未満を切り捨てることとし、手数料や税金等は考慮しないものとする。

〈年２％の各種係数〉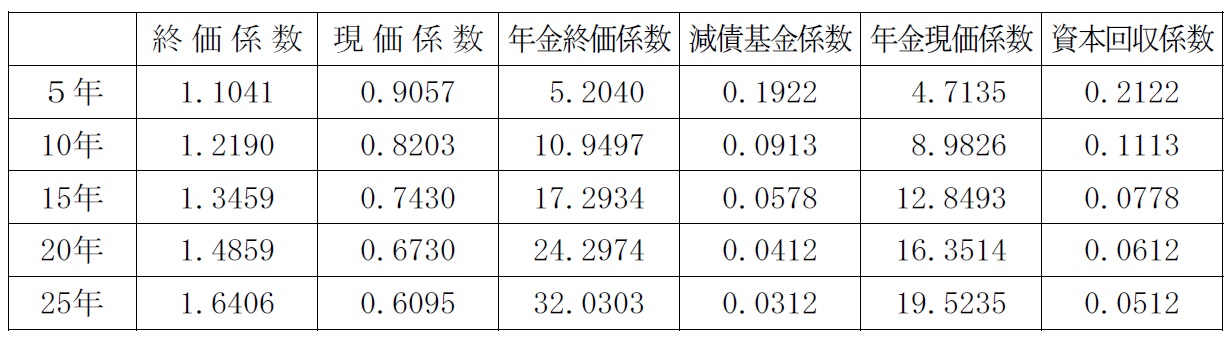


1) 271千円

2) 300千円

3) 317千円

4) 323千円

各種係数に関する問題です。

年利2.0％で複利運用しながら、15年間毎年60万円を取り崩すために、65歳時にいくら必要か？、を計算式に表すと、以下の通りです。
毎年受け取る年金額（取り崩す額）×年金現価係数＝元金
※年金現価係数は、元本を一定利率で複利運用しながら毎年一定額を取り崩す場合、現在の元本がいくら必要かを計算するときに使います。
よって、予定金額＝60万円×12.8493＝770.958万円

次に、20年間年利2.0％で複利運用しながら、目標額770.958万円を積み立てる場合に、必要な毎年の積立額はいくらか？ということですから、これを計算式に表すと、
目標額×減債基金係数＝毎年の積立額
※減債基金係数は、一定期間一定利率で複利運用しながら目標額を積み立てる場合、毎年いくら積み立てるかを計算するときに使います。
よって、770.958万円×0.0412＝31.763…→31.7万円（1,000円未満切捨て）

なお、もし問題文に減債基金係数が提示されていない場合には、将来の積立額合計を年金終価係数で割ることでも算出可能です。

よって正解は、3

この問題と似ている問題を検索してみよう！「検索」ボタンをクリック！

• このサイト内を検索

＜FP対策通信講座＞

●LECのFP講座（キーワード検索欄で「1級」と検索）　⇒　FP（ファイナンシャル・プランナー）サイトはこちら

●1級FP技能士（学科試験対策）のWEB講座　⇒　１級ＦＰ技能士資格対策講座（資格対策ドットコム）

●通勤中に音声学習するなら　⇒　ＦＰ 通勤講座

●社労士・宅建・中小企業診断士等も受けるなら　⇒　月額定額サービス【ウケホーダイ】