問14　2022年9月実技（資産設計）

恵子さんの姉の佐藤さんは、発行日に購入した下表の個人向け国債（額面２００万円）を２０２２年９月１日に全額中途換金した。この国債の中途換金時の佐藤さんの受取金額として、正しいものはどれか。なお、計算過程および解答で円未満の端数が生じた場合は切り捨てること。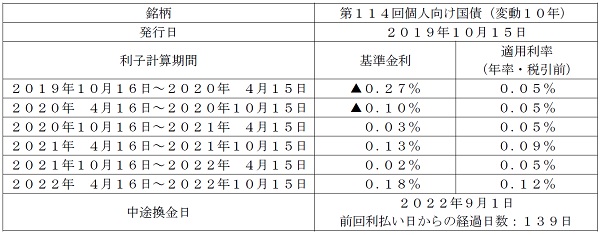



＜計算に際しての留意点＞
・ 経過利子相当額については、１年を３６５日とし、日割りにより計算すること。
・ 中途換金調整額の利子の計算期間については、便宜的に、６ヵ月／１２ヵ月として計算すること。
・ 中途換金調整額は、便宜的に、「直前２回分の各利子（税引前）相当額×０.８（復興特別所得税は考慮しない）」として計算すること。

１．１,９９９,５１３円

２．１,９９９,６１１円

３．１,９９９,７９３円

４．２,０００,２５０円

個人向け国債に関する問題です。

個人向け国債の中途換金時の受取額の計算式は、
受取額＝額面金額＋経過利子相当額−直前2回分の利子相当額×0.79685
です（2013年1月10日受渡分以降、復興特別所得税により「0.8」から「0.79685」となりました）。
ただし、本問では便宜上「0.79685」を「0.8」として計算するように指示があります。

まず、経過利子相当額とは、中途換金時に直近の利払い日以降の利子相当額が保有期間に応じて日割り計算されたものです。
国債を購入すると半年ごとに利払いがありますが、中途換金しても直近の利払い以降の保有日数（経過日数）もカウントしてくれるわけです。

個人向け国債は、3年固定・５年固定・10年変動のいずれも、毎月発行で（2013年10月分までは5年物と10年物は年4回発行）、利払い日は発行月と発行月の6ヵ月後の各15日です。よって、2019年10月発行の変動10年を購入して2022年9月1日に全て中途換金した場合、直近の利払い日は2022年4月15日で、その翌日4月16日から9月1日までの日数＝経過日数139日（適用利率0.12％）というわけです。

従って、経過利子相当額＝額面200万円×0.12％×139日／365日＝913.9…　
→913円（円未満切捨て）

次に、中途換金調整額＝直前2回分の利子相当額×0.8　で、直近の2回分の利払い日は2022年4月15日（適用利率0.05％）と2021年10月15日（適用利率0.09％）です。
また、利子相当額は半年分（6／12ヵ月）ですから、
中途換金調整額＝(200万円×0.05％×6／12ヵ月+200万円×0.09％×6／12ヵ月)×0.8＝1,120円

従って中途換金による受取額は、
額面200万円+913円−1,120円＝1,999,793円

以上により正解は、３．１,９９９,７９３円

この問題と似ている問題を検索してみよう！「検索」ボタンをクリック！

• このサイト内を検索

＜FP対策通信講座＞

●LECのFP講座（キーワード検索欄で「1級」と検索）　⇒　FP（ファイナンシャル・プランナー）サイトはこちら

●1級FP技能士（学科試験対策）のWEB講座　⇒　１級ＦＰ技能士資格対策講座（資格対策ドットコム）

●通勤中に音声学習するなら　⇒　ＦＰ 通勤講座

●社労士・宅建・中小企業診断士等も受けるなら　⇒　月額定額サービス【ウケホーダイ】